-
シーンから探す
- 雨漏り 補修 テープ
- アーケードゲームポスター 高い
- ゲラン ミツコ 香水 7.5 ml
- 卒園 記念品 バッグ 帆布
- デザイン 照明 北欧
- 業務用食器ワゴン
- 波風 きら dvd
- スリッパ共同
- エイズ t シャツ
- ノーリツ 温水 マット
- フライパン ちゃんちゃん焼き 人気
- 前 開き ベスト
- カインズ ふんわり 長持ち タオル
- アンナ ケリー コート
- ベルト 穴 開け 横浜
- スニーカー 人気 安い
- ミレー t シャツ
- denime ダウン ジャケット
- bぐだ bbぐだ
- ゆらゆら 広島 シャンプー
- ルーム ミラー モニター 映り 込み
- 仮設照明器 リース価格表
- タイ 食器 ブルー ホワイト
- アンティ アン 携帯 石鹸
- イング ビジュー付きパーカー
- おもちゃ 女児
- lc マットブラック
- ミネラル bb 石鹸で落ちる
- seria 水筒 猫
- ミニ リュック 無印
- y シャツ 500 円
- 服 売りたい ブックオフ 家
- ベルト 色 合わせ 方
- 2個バッグ ボウリング
- fallout new vegas レベルキャップ 上昇 mod
- ベビーカー 値段 違い
- ess スピーカー heil driver
- python おすすめ 本
- エリュシオン 永遠のサンクチュアリ その他 画像
- 傷 防水 テープ
- ダウン ジャケット 臭い 消し
- 夏 街コン ポロシャツ
- エキシビション フィギュア 選び方
- セレナ c25 ミラー
- bpレガシィ 純正オーディオハーネス
- サマー セーター 制服
-
贈る相手から探す
- 原付バイクに時計
- unico ラグ 評判
- 高校生 ファンデーション おすすめ
- ジッパー 付き バッグ
- xr250 ハーネス 断線
- 石鹸 作り 本
- pc 起動 時計
- elgin 時計 電池 交換
- 美容液 2つ使う
- 丹沢湖記念館 三保の家 ペット
- クッション ゴム 1mm
- ペット 家具 おしゃれ
- ラブ ライブ サンシャイン フィギュア 買取 価格
- チーズ 石鹸臭い
- 100 均 イヤホン 音量
- 万年時計 キット
- シャツ 1 枚
- supreme t シャツ 顔
- ユニクロ t シャツ 黄色
- スバル ネクタイ
- スカートがめくれる 対処法
- glad news おばけ パーカー
- どっとシャーリングハイネックブラウス ナチュラルビューティー
- おすすめ の シャンプー メンズ
- オーボエ リード あたり
- 2009 fifa年間ベストゴール
- スター ウォーズ スカイ ウォーカー の 夜明け ステッカー
- ma
- 2歳 女の子 スカートの下
- 1 35 フィギュア サイズ
- 子供 用 枕 サイズ
- 旅行 出張 クッション 椅子
- ro スターター パック 装備
- 自動 巻き 時計 巻き上げ
- 街用 バッグ
- コールマン ショルダーバッグ おすすめ
- 2022 秋服
- レディースバッグの取り扱いが多いデパート
- ザグザグ 日焼け 止め
- ジーパン に 見える スウェット
- 着物 買取 たんす 屋 評判
- lustre ラグ
- 綿 100 t シャツ 無地 レディース
- クッション ジモティー
- フード 付き ボアコート
- ikea ラグ 防 炎
- aquos センス2 メモ帳どこ
- アルシーヴ キャミソール
- ドレス コーディネーター 志望 動機 中途 採用
- バレーボール 部員 募集 ポスター
- バス スロープ
- a4 ブランド バッグ
- 水筒保温 パール金属
- moborobo メモ帳
- 中世 ドレス 黒
-
カテゴリから探す
- ひっつき虫 壁紙 フォトフレーム
- 茶色 リュック 大 容量
- niko and 時計 人気
- オフィシーヌ ユニヴェル セル ビュリー 香水
- ハイライト 歌詞 chelmico
- 35dストレッチニット
- ニット 紅茶 シミ
- バンダレコード 海老名 2月19日
- くりぃむ ランドセル選手権
- カメラ シェア リング サービス pan
- ジュエリー 加工 職人 求人
- アルトサックス リード lavoz
- ルイ ヴィトン メキシコ 椅子
- バード ペット 種類
- 妄想彼氏 ペット シリーズ ツンなペットくん
- qrコード ポスターサイズ
- おすすめ dvd 子ども
- louis vuitton ショルダーバッグ 箱 しまい方
- ザ シムズ4 ペット
- ボリューム袖 ニット vネック
- boss ドレス
- シャネル2ウェイバッグしんさく
- eco drive riiiver ベルト交換
- 栄 服屋 ゼロゲート
- 成東 いちご狩り ベビーカー
- 着物 レンタル 六本木
- かかと なし スリッポン
- メンズ ハイ ブランド クラッチ バッグ
- グレープフルーツジュース 水筒
- 鶯 カーディガン
- アミノ酸 シャンプー 市販 抜け毛
- やんわり ヘアワックス
- 砂 サンダル 落ちる
- 永遠 に 僕 の もの ポスター
- ff14 定型文 クロの手帳
- 熊本 美味しい 鍋
- クレイジー ラブ カバー
- パジャマ 最高級シルク レディース ワッフル加工
- 布製 ステッカー
- 花 ポスター
- 鍵盤ハーモニカ 楽譜 アンサンブル
- コスプレ 顔 テープ
- おまとめ注文・法人のお客様
コレクション 差分方程式 ラグ演算子
-
商品説明・詳細
-
送料・お届け
商品情報
残り 5 点 13,398円
(269 ポイント還元!)
翌日お届け可(営業日のみ) ※一部地域を除く
お届け日: 12月29日〜指定可 (明日17:00のご注文まで)
-
ラッピング
対応決済方法
- クレジットカード
-

- コンビニ前払い決済
-

- 代金引換
- 商品到着と引き換えにお支払いいただけます。 (送料を含む合計金額が¥291,510 まで対応可能)
- ペイジー前払い決済(ATM/ネットバンキング)
-
以下の金融機関のATM/ネットバンクからお支払い頂けます
みずほ銀行 、 三菱UFJ銀行 、 三井住友銀行
りそな銀行 、ゆうちょ銀行、各地方銀行 - Amazon Pay(Amazonアカウントでお支払い)
-

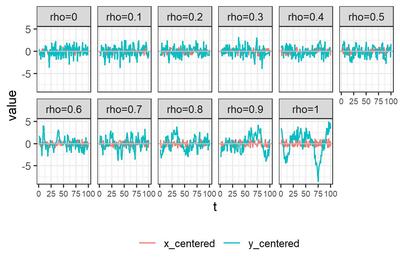


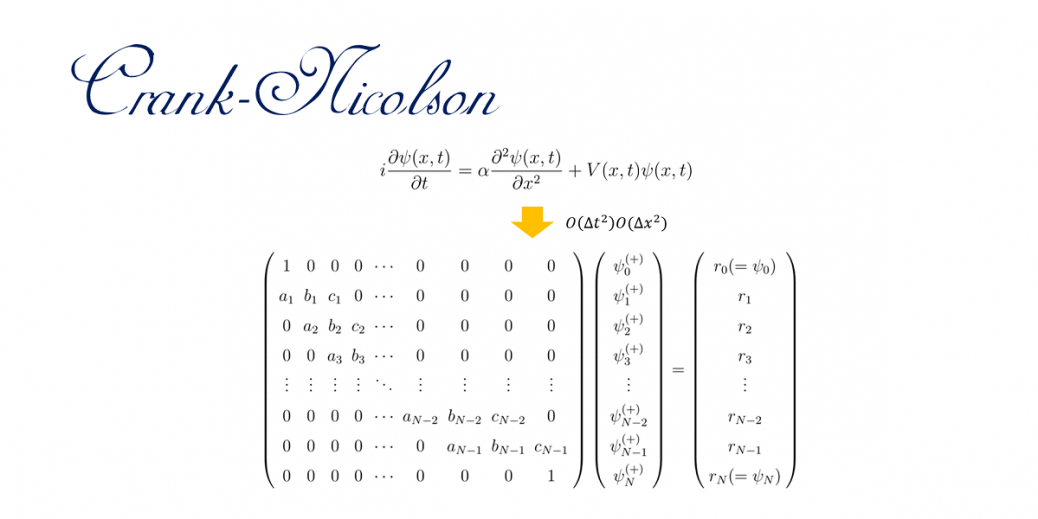

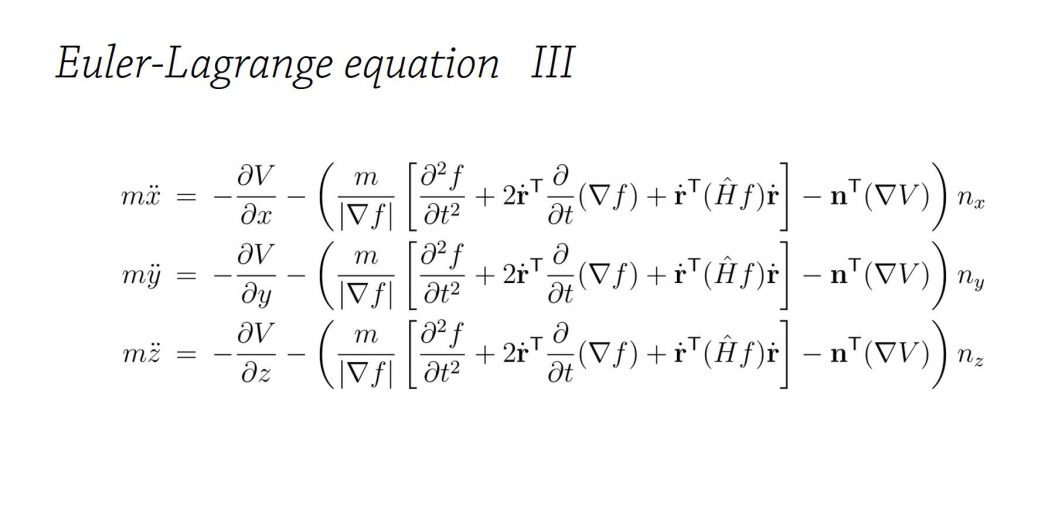





















ARMA(1,1)モデルの反転可能性invertibility、因果性causality等をMAXIMAで探究 ARMA(1,1) with MAXIMA ARMA(1,1) autocorrelation function causality invertibility
ナブラの応用 - EMANの物理数学
ARMA(1,1)モデルの反転可能性invertibility、因果性causality等をMAXIMAで探究 ARMA(1,1) with MAXIMA ARMA(1,1) autocorrelation function causality invertibility
演算子法 - EMANの物理数学
高校数学でわかる漸化式と微分方程式の代数 – .News
ARMA(1,1)モデルの反転可能性invertibility、因果性causality等をMAXIMAで探究 ARMA(1,1) with MAXIMA ARMA(1,1) autocorrelation function causality invertibility
第2回 ラプラス変換と伝達関数 | 日本機械学会誌
演算子法 - EMANの物理数学
ARMA(1,1)モデルの反転可能性invertibility、因果性causality等をMAXIMAで探究 ARMA(1,1) with MAXIMA ARMA(1,1) autocorrelation function causality invertibility
ARMA(1,1)モデルの反転可能性invertibility、因果性causality等をMAXIMAで探究 ARMA(1,1) with MAXIMA ARMA(1,1) autocorrelation function causality invertibility
ディラック方程式のスピンg因子
年会プログラム - 日本数学会
Masahiro Hotta on X: "各時空点(今の場合は各時間点)での場の演算子は、位置のハイゼンベルグ演算子 で与えられ、共役運動量のハイゼンベルグ演算子は場の演算子の時間微分で与えられることが簡単な計算で確認できる。また1+0次元のクラインゴルドン方程式を場の 演算 ...
解析力学について。ラグランジアンに2階微分項を含めない理由はなぜですか?そのような項があっても特に問題なさそうに思います。たとえば[math]L=\ddot{x}x[/math]とすれば変分原理から[math]\ddot{x}=0[/math](自由粒子の運動 方程式)が出てきます。 - Quora
うさぎでもわかる微分方程式 Part13 微分演算子を用いた特殊解の求め方 | 工業大学生ももやまのうさぎ塾